Instruções
O projecto deverá ser resolvido em grupos de três alunos e entregue no dia 21 de Dezembro de 2006 (5ª feira), entre as 15:00 e as 16:00 na sala P1.12 (sala de dúvidas do DM). Os alunos que não puderem comparecer neste horário podem entregá-lo no mesmo dia entre as 12:00 e as 13:00 no mesmo local.
A resolução deverá conter:
- um relatório incluindo as principais opções de implementação, a listagem do programa e exemplos de execução do programa desenvolvido;
-
um CD contendo os ficheiros de código desenvolvidos (módulo
mpole programa principal).
Módulos
Módulos
Introdução
Na construção de estradas em terreno montanhoso, o traçado da estrada tem de ter em conta o relevo do terreno que atravessa. Por um lado, fazer aterros, viadutos e túneis é mais caro que construir ao nível do terreno, mas em contrapartida quanto mais curto for o percurso mais barata fica a construção da estrada. Para determinar o traçado da estrada é necessário ter estes dois factores em conta e tentar encontrar um percurso que por um lado minimize as variações em altura dos terrenos que atravessa, mas que também não faça desvios demasiadamente grandes.
Na figura da esquerda mostra-se o relevo dum terreno quadrado (a gradação de cor num ponto corresponde à cota desse ponto). Pretende-se construir uma estrada que atravesse este terreno do canto inferior esquerdo ao canto superior direito; por conveniência, convencionou-se tomar para unidade de comprimento a medida do lado do terreno. A figura da direita mostra um exemplo dum traçado possível para a estrada que representa um bom compromisso entre os dois factores acima descritos. Note que esta estrada é mais comprida que uma linha recta, mas em compensação evita variações grandes de nível.

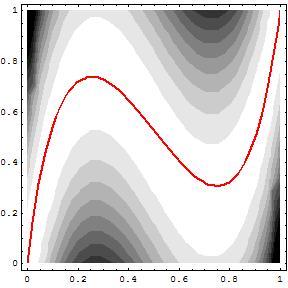
Problema
O objectivo deste projecto é, utilizando princípios de Programação Evolutiva, desenvolver em F um programa para encontrar uma solução para o problema acima.
O relevo do terreno é dado por uma função Φ : [0,1]×[0,1]→ℜ. No exemplo da figura acima, Φ(x,y) = (y−x/3(32x2−48x+19))2. A estrada é uma curva parametrizada por dois polinómios p,q : [0,1]→[0,1] de grau máximo gm, ou seja, é o conjunto dos pontos {(p(t),q(t)) : t∈[0,1]}.
Para resolver o problema, começa-se por gerar no instante zero uma população de ν indivíduos, todos representando um caminho em linha recta (ou seja, p(t) = q(t) = t), e fazê-la evoluir até ao instante final τ. A cada indivíduo z está associado um conforto φ(z)=e−η∑i=1N|Φ[p(i/N),q(i/N)]−Φ[p(i−1/N),q(i−1/N)]|, que intuitivamente é proporcional à soma das variações médias de declives ao longo de N troços do percurso.
Cada indivíduo z evolui de acordo com o seu conforto através dos mecanismos aleatórios seguintes.
- Morte, com tempo médio −log(1−φ(z))μ entre eventos.
- Reprodução, com tempo médio −log(φ(z))ρ entre eventos. A reprodução é sempre efectuada com o melhor indivíduo da população. Da reprodução surge um novo indivíduo cujo caminho é parametrizado por polinómios obtidos da seguinte forma: primeiro, toma-se para coeficiente de xk a média aritmética dos coeficientes de xk nos polinómios correspondentes dos dois progenitores; em seguida divide-se o polinómio obtido pelo seu valor no ponto 1.
- Mutação, com tempo médio −log(φ(z))δ entre eventos. Uma mutação consiste em alterar um coeficiente (que não o do termo independente) ou em um ou em ambos os polinómios; o novo coeficiente é um número aleatório no intervalo de amplitude 2log(φ(z))ω/1+gm centrado no valor original do coeficiente. Cada polinómio assim obtido é de novo dividido pelo seu valor no ponto 1.
Programa
O programa a desenvolver deve resolver este problema para a função de relevo Φ acima definida. Para tal, deve:-
receber interactivamente o conjunto seguinte de dados:
- grau máximo gm dos polinómios a utilizar;
- instante final τ(>0) da evolução;
- lista de parâmetros ν,N,η,μ,ρ,δ e ω;
- devolver o indivíduo z com maior conforto e os coeficientes dos polinómios que parametrizam o seu caminho;
- mostrar, quando solicitado, o resultado de 20 observações da população igualmente espaçadas no tempo. Cada observação deve incluir o instante actual, o número de eventos já realizados, a dimensão da população, os coeficientes dos polinómios que parameterizam o caminho do melhor indivíduo encontrado e o conforto deste indivíduo.
- Comece por identificar os objectos de trabalho, nomeadamente polinómio, indivíduo e população.
- Implemente a camada dos polinómios sobre a camada básica da linguagem F. As restantes camadas serão disponibilizadas posteriormente (ver Apêndice B).
- Desenvolva de seguida o programa abstracto pretendido sobre a camada que disponibiliza estes objectos.
- Integre o programa obtido em 3 com o módulo desenvolvido em 2.
-
Experimente o programa desenvolvido em 4 com diversos conjuntos de dados à sua escolha. Em particular, considere o conjunto:
- grau máximo dos polinómios: gm=5;
- τ=4;
- parâmetros de evolução: ν=10, N=1000, η=3/4, μ=200, ρ=δ=1 e ω=10.
- Altere a função de relevo considerada e experimente o programa.
Apêndice A
Relativamente às variáveis aleatórias, recorra à subrotinarandom_number da linguagem F para implementar as seguinte subrotinas:
-
para simular uma variável aleatória exponencial com valor médio m use a subrotina:
subroutine vexp(m,x)
real, intent(in) :: m
real, intent(out) :: x
call random_number(x)
x=-m*log(x)
end subroutine vexp -
para gerar aleatoriamente um número inteiro entre 1 e k use a subrotina:
subroutine randinteger(k,r)
integer, intent(in) :: k
integer, intent(out) :: r
real :: x
call random_number(x)
r=int(1+k*x)
end subroutine randinteger -
para gerar aleatoriamente um número entre a e b com distribuição uniforme use a subrotina:
subroutine randunif(a,b,t)
real, intent(in) :: a,b
real, intent(out) :: t
real :: x
call random_number(x)
t=a+(b-a)*x
end subroutine randunif
Apêndice B
Oportunamente serão aqui disponibilizados os módulos seguintes:-
Módulo
mind: disponibiliza o tipo de dadosinde as seguintes funções e subrotinas sobre este tipo de dados:-
fazind(p,q,tm,tr,td,cf,z): subrotina que recebe nos parâmetros de entradapeqde tipopoletm,tr,tdecfde tiporeal, respectivamente, dois polinómios, um tempo de morte, um tempo de reprodução, um tempo de mutação e um conforto e devolve no parâmetro de saídazde tipoindum indivíduo com estas características; -
px(z,p): subrotina que recebe no parâmetro de entradazde tipoindum indivíduo e devolve no parâmetro de saídapde tipopolo polinómio que parameteriza horizontalmente o caminho associado a esse indivíduo (p); -
py(z,q): subrotina que recebe no parâmetro de entradazde tipoindum indivíduo e devolve no parâmetro de saídaqde tipopolo polinómio que parameteriza verticalmente o caminho associado a esse indivíduo (q); -
tm(z): função que recebe no parâmetrozde tipoindum indivíduo e devolve o seu tempo de morte (de tiporeal); -
tr(z): função que recebe no parâmetrozde tipoindum indivíduo e devolve o seu tempo de reprodução (de tiporeal); -
td(z): função que recebe no parâmetrozde tipoindum indivíduo e devolve o seu tempo de mutação (de tiporeal); -
conf(z): função que recebe no parâmetrozde tipoindum indivíduo e devolve o seu conforto (de tiporeal); -
mts(z): função que recebe no parâmetrozde tipoindum indivíduo e devolve o menor dos seus três tempos (morte, reprodução ou mutação); -
evt(z): função que recebe no parâmetrozde tipoindum indivíduo e devolve o tipo de evento que esse indivíduo vai realizar:Mse for uma morte,Rse for uma reprodução eDse for uma mutação. Nota: o valor devolvido é de tipocharacter(len=1).
-
-
Módulo
mpop: disponibiliza o tipo de dadospope as seguintes funções e subrotinas sobre este tipo de dados:-
nova(): função sem parâmetros que devolve a população vazia; -
insere(p,z): subrotina que recebe no parâmetro de entrada/saídapde tipopopuma população e no parâmetro de entradazde tipoindum indivíduo e devolve empa população com o novo indivíduo inserido; -
proximo(p,z): subrotina que recebe no parâmetro de entradapde tipopopuma população e devolve no parâmetro de saídazde tipoindo primeiro indivíduo da população, isto é, o indivíduo com menor tempo; -
apaga_p(p): subrotina que recebe no parâmetro de entrada/saídapde tipopopuma população e devolve empessa população sem o primeiro indivíduo (proximo); -
melhor(p,z): subrotina que recebe no parâmetro de entrada/saídapde tipopopuma população e devolve no parâmetro de saídazde tipoindo indivíduo com maior conforto; -
vazia(p): função que recebe no parâmetropde tipopopuma população e devolve.true.se essa população estiver vazia,.false.caso contrário; -
tam(p): função que recebe no parâmetropde tipopopuma população e devolve o seu tamanho (número de indivíduos).
-
Os módulos mind e mpop pressupõem a existência de um módulo mpol. Este módulo deve incluir, entre outras, uma definição do tipo pol e as seguintes funções e subrotinas:
-
novo(g,p): subrotina que recebe no parâmetro de entradagde tipointegero grau do polinómio a criar e devolve empde tipopolo polinómio de graugem que todos os coeficientes são 0; -
atr(p,i,x): subrotina que recebe no parâmetro de entrada/saídapde tipopolum polinómio e nos parâmetros de entradaiexde tipointegerereal, respectivamente, dois valores e altera o coeficiente do termo de ordemidepparax; -
coef(p,i,x): subrotina que recebe no parâmetro de entrada/saídapde tipopolum polinómio e no parâmetro de entradaide tipointegerum valor e devolve no parâmetro de saídaxde tiporealo coeficiente do termo de ordemi; -
val(p,x,r): subrotina que recebe no parâmetro de entrada/saídapde tipopolum polinómio e no parâmetro de entradaxde tiporealum valor e devolve no parâmetro de saídarde tiporealo valor do polinómiopemx(se este valor estiver acima de 1, a subrotina deve devolver 1; se o valor estiver abaixo de 0, a subrotina deve devolver 0); -
norm(p): subrotina que recebe no parâmetro de entrada/saídapde tipopolum polinómio e devolve nesse parâmetro o polinómio dividido pelo seu valor no ponto 1; -
conv(p,v): subrotina que recebe no parâmetro de entrada/saídapde tipopolum polinómio e devolve no parâmetro de saídavum vector de números reais de comprimento gm+1 contendo na posiçãoi+1o coeficiente do termo de ordemi.
Note que é fundamental que a especificação anterior seja respeitada para que os módulos mpop e mind fornecidos funcionem!